Fungsi eksponen adalah fungsi dimana peubah sebagai pangkat.
Fungsi eksponen f(x)=ax memiliki syarat basis (bagian yang dipangkatkan) harus positif kecuali 1, dapat ditulis sebagai berikut.
a>0 dan a≠1
Fungsi ini memetakan x bilangan real ke f(x)=ax
Grafik Fungsi Eksponen
Grafik fungsi eksponen berbentuk kurva dimana salah satu ujungnya mendekati asimtot. Contoh fungsi eksponen adalah sebagai berikut.
f(x)=2x
Grafik dari fungsi ini dapat diperoleh salah satunya dengan terlebih dahulu kita tentukan pasangan titik yang dilaluinya kemudian kita gambar kurva yang melalui titik-titik tersebut.
Pasangan titik-titik yang dilalui contoh fungsi di atas dapat kita nyatakan dalam bentuk tabel berikut.
| x | y=f(x)=2x | (x,y) |
|---|---|---|
| -1 | 2-1=0.5 | (-1,0.5) |
| 0 | 20=1 | (0,1) |
| 1 | 21=2 | (1,2) |
| 2 | 22=4 | (2,4) |
| 3 | 23=8 | (3,8) |
Gambarkan pasangan titik-titik tersebut pada koordinat kartesius dan hubungkan dengan kurva, grafiknya adalah seperti berikut.
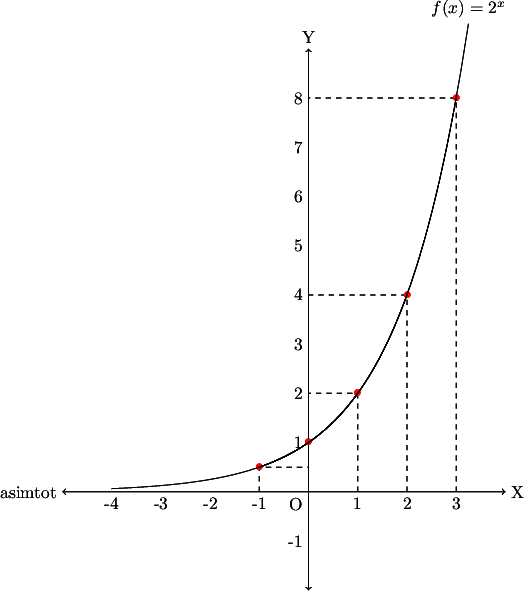
Pada grafik di atas, sumbu X merupakan asimtot. Artinya sumbu X ini didekati oleh kurva tetapi sumbu X dan kurva tidak pernah berpotongan.
Transformasi Grafik Fungsi Eksponen
Fungsi eksponen pada contoh di atas merupakan salah satu contoh fungsi eksponen sederhana. Modifikasi terhadap fungsi mengakibatkan bentuk dasar kurva fungsi eksponen berubah. Salah satu perubahan yang dapat diamati adalah bergesernya kurva ke atas/bawah atau ke kanan/kiri. Transformasi ini dapat dilihat dari bilangan yang dijumlahkan pada peubah x di pangkat atau pada fungsi secara keseluruhan.
Perhatikan bentuk fungsi eksponen berikut.
f(x)=ax±m±n
Nilai m dan n menggeser kurva eksponen dengan ketentuan sebagai berikut.
- +m menggeser kurva ke kiri
- -m menggeser kurva ke kanan
- +n menggeser kurva ke atas
- -n menggeser kurva ke bawah
Perhatikan kurva g(x)=2x+1 dan h(x)=2x-1 terhadap f(x)=2x berikut ini.

Fungsi g(x) bergeser ke sebelah kiri akibat dari peubah pada eksponen ditambah bilangan. Sedangkan fungsi h(x) bergeser ke bawah akibat dari pengurangan fungsi oleh bilangan.
Pada fungsi h(x) asimtot tidak lagi di sumbu X. Hal ini karena bergesernya fungsi ke bawah, asimtot pun bergeser ke bawah. Asimtot fungsi h(x) terletak pada y=-1 yang terletak di bawah sumbu X.
Penentuan asimtot didasarkan pada konstanta yang dijumlahkan atau dikurangkan pada fungsi dasarnya. Pada contoh di atas fungsi h(x) konstantanya adalah -1. Asimtot juga diperoleh ketika fungsi eksponen dasar (ax) bernilai nol.
Sekian pembahasan mengenai fungsi eksponen. Semoga membantu Kamu memahami materi ini dan yang terkait lainnya.
 Oleh Opan
Oleh Opan
Dipostkan August 09, 2020
Seorang guru matematika yang hobi ngeblog dan menulis. Dari ketiganya terwujudlah website ini sebagai sarana berbagi pengetahuan yang saya miliki.