Konsep jarak antara dua objek selalu berdasar pada jarak antara dua titik. Baik jarak antara titik dan garis , titik dan bidang, garis dan garis, garis dan bidang, serta bidang dan bidang. Kali ini saya akan membahas tentang jarak antara titik dan bidang pada bangun ruang (dimensi tiga). Coba perhatikan gambar di bawah ini.

Gambar di atas menunjukkan sebuah titik A dan sebuah bidang alpha. Jarak antara titik A dengan bidang alpha adalah panjang ruas garis AA' dimana titik A' merupakan proyeksi titik A pada bidang alpha. Untuk memahami proyeksi, perhatikan penjelasan berikut ini.
Andaikan bidang alpha adalah sebuah lantai dan tepat tegak lurus lantai di atas titik A dipasang sebuah lampu. Jika lampu dinyalakan maka akan ada bayangan titik A pada lantai (bidang alpha).
Nah, bayangan tersebut merupakan proyeksi titik A pada bidang alpha. Dengan demikian, proyeksi titik A pada bidang alpha, yaitu A' dapat digambarkan sebagai berikut.

Ruas garis AA' tersebut tegak lurus terhadap bidang alpha. Artinya, ruas garis AA' tegak lurus terhadap semua garis pada bidang alpha yang melalui titik A'.
Itulah konsep dasar mengenai jarak antara titik dan bidang. Sekarang, kita lanjutkan pembahasan mengenai bagaimana menghitung jarak antara titik dan bidang. Langkah pertama untuk menghitung jarak antara titik dan bidang adalah mencari jarak antara titik tersebut dan garis pada bidang yang melalui proyeksi titik pada bidang. Berarti nyambung dengan konsep jarak antara titik dan garis. Selanjutnya, hitung jaraknya dengan menggunakan konsep jarak antara titik dan garis.
Untuk lebih memahaminya, berikut saya sajikan contoh soal jarak antara titik dan bidang beserta pembahasannya. Check this out!
Perhatikan gambar kubus ABCD.EFGH dengan panjang rusuk 6 satuan berikut ini.

Tentukan jarak antara titik A dan bidang BCGF!
Untuk menghitung jaraknya, kita perlu mengetahui dulu dimana letak proyeksi titik A pada bidang BCGF. Agar mudah membayangkannya, berikut adalah gambarnya.

Dari gambar tersebut, terlihat bahwa proyeksi titik A pada bidang BCGF terletak pada titik B yang terletak pada ruas garis BF. Artinya jaraknya dapat diperoleh dengan cara menghitung jarak antara titik A dan garis BF. Karena AB tegak lurus dengan BF maka jaraknya sama dengan panjang ruas garis AB yaitu 6 satuan.
Tentukan jarak antara titik A dan bidang BDHF!
Seperti biasa, untuk menghitung jaraknya terlebih dahulu kita tentukan proyeksi titik A pada bidang BDHF. Berikut adalah gambarnya.

Dari gambar tersebut terlihat bahwa proyeksi titik A pada bidang BDHF terletak di pertengahan ruas garis BD. Artinya, jarak antara titik A dan bidang BDHF sama dengan jarak antara titik A dan ruas garis BD. Karena ruas garis AC tegak lurus ruas garis BD (diagonal persegi berpotongan tegak lurus) dan ruas garis AA' berimpit dengan ruas garis AC maka jarak antara titik A dengan ruas garis BD sama dengan jarak antara titik A dan titik potong ruas garis AC dan ruas garis BD yang nilainya sama dengan setengah panjang ruas garis AC dimana AC merupakan diagonal bidang.

Tentukan jarak antara titik A dan bidang BDE!
Perhatikan gambar di bawah ini.

Proyeksi titik A pada bidang BDE terletak pada ruas garis EO dengan O titik tengah ruas garis BD. EO merupakan garis tinggi segitiga BDE di titik E. Misalkan proyeksinya adalah titik A', titik AA' ini berimpit dengan ruas garis AG dan ruas garis AG (juga AA') tegak lurus ruas garis EO. Untuk menghitung jaraknya kita perlu menggunakan konsep kesebangunan dan teorema pythagoras.
Dari gambar di atas diketahui panjang AO sama dengan setengah panjang AC yang merupakan diagonal bidang. Segitiga AOE sebangun dengan segitiga AOA' (A' adalah titik potong AG dan EO).

Menurut kesebangunan, diperoleh

Dengan demikian
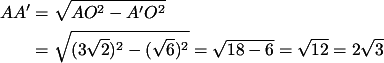
Perhatikan bahwa AA' (jarak antara titik A dan bidang BDE) hasilnya sama dengan 1/3 dari panjang AG (diagonal ruang). Untuk kasus yang sama, yaitu jarak antara titik pada kubus dengan segitiga diagonal bidang sebenarnya kita tidak perlu menghitung dengan cara serumit di atas. Perhatikan gambar di bawah ini.

Pada gambar di atas, jika kita gambarkan persegi panjang ACGE akan menjadi seperti berikut ini.

Perhatikan bahwa ruas garis AG dibagi menjadi tiga bagian yang sama pajang oleh ruas garis EO dan CO'. dan ruas garis AG ini tegak lurus terhadap keduanya. Dengan demikian, panjang ruas garis AA' (yang merupakan jarak antara titik A dan bidang BDE) sama dengan 1/3 dari panjang ruas garis AG. Hasil ini sama dengan pembahasan di atas, yaitu panjang AA' adalah 1/3 dari panjang ruas garis AG. Hubungan ini bersifat umum dan dapat dinyatakan sebagai berikut.
Jarak terdekat suatu titik pada kubus terhadap segitiga diagonal bidang adalah 1/3 dari panjang diagonal ruang, sedangkan jarak terjauh suatu titik terhadap segitiga diagonal bidang adalah 2/3 dari panjang diagonal ruang.
Jarak antara titik G dan bidang BDE merupakan contoh jarak terjauh suatu titik terhadap segitiga diagonal bidang yang panjangnya 2/3 dari panjang diagonal bidang.
Sekian pembahasan mengenai jarak antara titik dan bidang pada bangun ruang (dimensi tiga). :-D
 Oleh Opan
Oleh Opan
Dipostkan April 04, 2013
Seorang guru matematika yang hobi ngeblog dan menulis. Dari ketiganya terwujudlah website ini sebagai sarana berbagi pengetahuan yang saya miliki.