Kalau denger kata "rumus" yang terbayang adalah "harus menghapal" dan mungkin beberapa orang berpikir "hebat banget ya orang yang nemuin rumus itu". Rumus tidak ditemukan begitu saja tetapi melalui serangkaian proses. Rumus matematika merupakan aturan umum untuk menyelesaikan permasalahan matematika.
Rumus yang ada sekarang dapat dibuktikan melalui pembuktian deduktif untuk menyatakan rumus tersebut benar-benar valid / sah dan berlaku secara umum. Salah satu rumus yang perlu dipahami dipahami dalam belajar matematika adalah rumus pangkat (eksponen). Mari kita bahas beberapa rumus terkait konsep pangkat atau eksponen.
Perkalian Bilangan Berpangkat
Perhatikan perkalian dua bilangan berpangkat berikut.
23x24
Apabila masing-masing pangkat di atas diuraikan ke dalam bentuk perkalian berulang, akan didapat bentuk berikut.
23x24=(2x2x2)x(2x2x2x2)
Hasil perkaliannya ternyata berbentuk perkalian berulang lagi.
23x24=2x2x2x2x2x2x2=27
Dari hasil di atas diperoleh hubungan bahwa hasil perkalian dua bilangan berpangkat adalah bilangan berpangkat yang lebih sederhana. Pangkat dari hasil perkaliannya ternyata berhubungan dengan pangkat dari masing-masing bilangan yang dikalikan. Perhatikan bahwa 7 = 3 + 4. Dari bentuk tersebut kita mendapat kesimpulan sementara sebagai berikut.
23x24=23+4=27
Perhatikan bahwa hubungan tersebut berlaku karena bilangan yang dipangkatkannya sama, yaitu 2. Itu merupakan syarat dalam menyederhanakan perkalian dari dua bilangan berpangkat.
Bentuk terakhir di atas jika diperumum akan menjadi seperti berikut.
amxan=am+n
Rumus ini juga berlaku secara umum untuk pangkat bilangan real. Pembuktian untuk bilangan real silakan sebagai latihan.
Pembagian Bilangan Berpangkat
Bagaimana dengan rumus pembagian dua bilangan berpangkat? Perhatikan contoh berikut.

Kalau kita perhatikan, hubungan antara pangkat dari masing-masing pembilang dan penyebut dengan pangkat hasil pembagiannya menunjukan pola sebagai berikut.

Secara umum bentuk sederhana dari pembagian bilangan berpangkat adalah sebagai berikut.

Pangkat Nol (0)
Bilangan nol merupakan bilangan yang istimewa. Inget bilangan nol, pasti inget dengan Al-Khawarizmi. Gosipnya, beliaulah yang memperkenalkan bilangan nol ini.
Bilangan nol bisa diperoleh dari pengurangan bilangan yang sama. Berarti, pangkat nol dapat kita peroleh dari hasil operasi pengurangan dua bilangan yang sama. Perhatikan pembuktian pangkat bilangan nol berikut.

Pembuktian di atas menunjukkan bahwa pangkat nol suatu bilangan sama dengan 1. Rumus yang digunakan pada pembuktian di atas adalah rumus pembagian bilangan berpangkat yang telah di bahas sebelumnya di atas.
Pangkat Negatif
Bilangan negatif merupakan invers dari bilangan positif terhadap operasi penjumlahan.
n+(-n)=0 ⇔ (-n)=0-n
Berarti pangkat -n bisa juga dituliskan sebagai 0 - n. Berikut ini adalah pembuktian rumus untuk pangkat negatif.

Rumus-Rumus Pangkat Lengkap

Contoh Soal Beserta Penyelesaian
Dalam bentuk pangkat positif,

Jawaban C
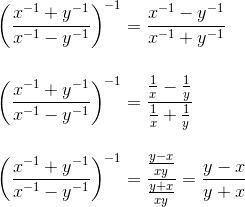
Demikian penjelasan singkat mengenai rumus-rumus pangkat. Semoga dapat membantu Kamu mempelajari konsep ini dan kaitannya dengan konsep lain.
 Oleh Opan
Oleh Opan
Dipostkan November 15, 2012
Seorang guru matematika yang hobi ngeblog dan menulis. Dari ketiganya terwujudlah website ini sebagai sarana berbagi pengetahuan yang saya miliki.